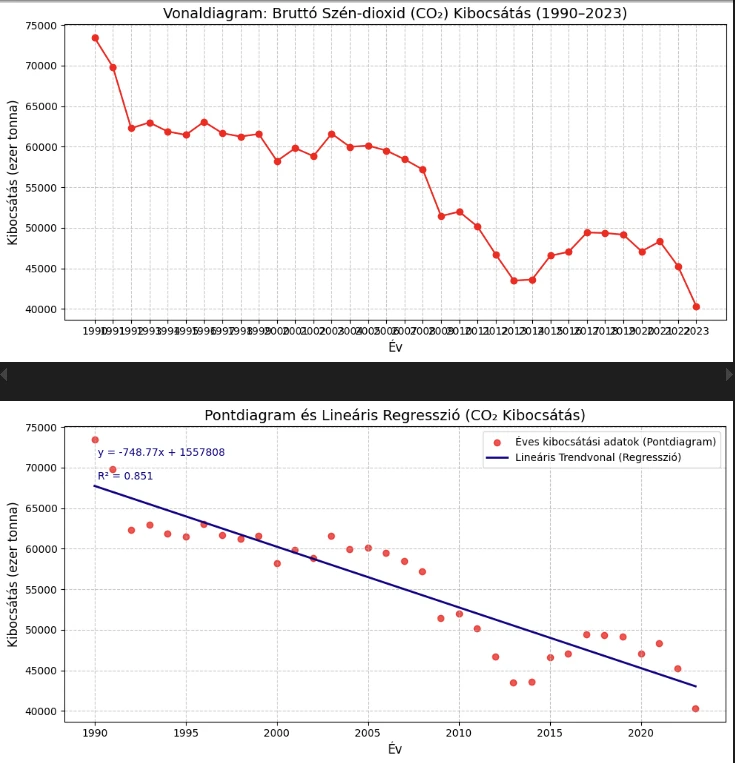
A projekt konkrét problémája: Tényekkel és megbízható matematikai modellel igazolható-e, hogy az elmúlt 33 évben Magyarországon fenntartható és mérhető csökkenés következett-e be a CO₂ kibocsátásban, és milyen mértékű ez az éves változás?
A probléma megoldásához egy Python alapú szkriptet használtam. Az elemzés automatizálásához a Pandas adatszerkesztő a Scikit-learn statisztikai és vizualizációhoz a Matplotlib könyvtárakat alkalmaztam. Ahogy most is látható, a program Lineáris Regressziós számítást végez az adatokon. Az R2 érték 0.851, ami statisztikailag is megerősíti a fő konklúziót: a magyar CO₂ kibocsátás átlagosan 748 ezer tonnával csökkent évente.
A fejlesztés során a legnagyobb nehézséget a teljes program felépítése jelentette, mert Pythont tanulóként a Pandas és a Scikit-learn ipari könyvtárak logikájának elsajátítása volt az igazi kihívás.
Összefoglalva: a projekt bizonyította, hogy a statisztikai elemzést és vizualizációt sikerült Python programnyelv segítségével megvalósítanom.
Követelmények a futtatáshoz:
- pandas
- matplotlib
- scikit-learn
- openpyxl (ha .xlsx-ből szeretnénk olvasni és nem elég a .csv)
A KSH-s mintafájl letölthető
innen:
https://files.probbi.com/stadat-kor0017-15.1.1.18-hu.csv
vagy innen:
https://drive.google.com/file/d/1ZR1jJiqiibQtS3Xvr-VisPHnC6ShNC6D/view?usp=drive_link
main.py
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import numpy as np
# A feltöltött CSV fájl neve. Írd át, ha XLSX-et használsz!
fajl_nev = "stadat-kor0017-15.1.1.18-hu.csv"
# 1. Adatok beolvasása, figyelembe véve a KSH struktúrát:
# - sep=';' pontosvesszős elválasztó
# - header=1 (a 2. sor a tényleges oszlopnév: Megnevezés, 1990, 1991, stb.)
# - encoding='iso-8859-2' (Ez a kódolás gyakran megoldja a magyar ékezetes hibákat KSH CSV-nél)
try:
df = pd.read_csv(fajl_nev, sep=';', header=1, encoding='iso-8859-2')
# Adatok átalakítása (Transzponálás: oszlopokból sorok)
evszam_oszlopok = [str(ev) for ev in range(1990, 2024)]
# Válasszuk ki a vizsgálandó sort: Szén-dioxid (CO2) (bruttó)
co2_sor = df[df['Megnevezés'].str.contains('Szén-dioxid \(CO2\) \(bruttó\)', na=False)].iloc[0]
# Hozzuk létre a tiszta (Év, Érték) párokat tartalmazó DataFrame-et
data = {
'Év': evszam_oszlopok,
# Tisztítás: eltávolítjuk a szóközt a számokból (pl. '73 427' -> '73427'), majd float-tá alakítjuk.
'Érték': co2_sor[evszam_oszlopok].astype(str).str.replace(' ', '', regex=False).astype(float)
}
df_tiszta = pd.DataFrame(data)
# Regresszióhoz való előkészítés
x = df_tiszta['Év'].astype(int).values.reshape(-1, 1) # X (Év)
y = df_tiszta['Érték'].values # Y (Érték)
print("Adatok sikeresen beolvasva és előkészítve a CO₂ kibocsátásról.")
except FileNotFoundError:
print(f"HIBA: A '{fajl_nev}' fájl nem található. Győződj meg róla, hogy a Notebookkal egy mappában van.")
except Exception as e:
print(f"HIBA történt az adatok beolvasása során: {e}. Próbáld meg az encoding='utf-8' beállítást.")
# Lineáris regresszió illesztése
model = LinearRegression()
model.fit(x, y)
y_pred = model.predict(x)
# Regressziós paraméterek
meredekseg = model.coef_[0]
metszet = model.intercept_
r_sq = model.score(x, y) # R²: Illeszkedés jósága
# Statisztikai Elemzés kiíratása
print("--- Statisztikai Elemzés: Bruttó CO₂ kibocsátás Magyarországon ---")
print(f"Vizsgált időszak: {df_tiszta['Év'].min()} - {df_tiszta['Év'].max()}")
print("-" * 50)
print(f"Átlagos éves kibocsátás: {np.mean(y):.0f} ezer tonna")
print(f"Minimum kibocsátás: {np.min(y):.0f} ezer tonna")
print(f"Maximum kibocsátás: {np.max(y):.0f} ezer tonna")
print("-" * 50)
print(f"Trend meredeksége (Éves átlagos változás): {meredekseg:.2f} ezer tonna/év")
print(f"Regressziós illeszkedés (R²): {r_sq:.3f}")
# 2. Vonaldiagram (Idősoros alakulás)
plt.figure(figsize=(10, 5))
plt.plot(df_tiszta['Év'], y, marker='o', linestyle='-', color='red')
plt.title("Vonaldiagram: Bruttó Szén-dioxid (CO₂) Kibocsátás (1990–2023)", fontsize=14)
plt.xlabel("Év", fontsize=12)
plt.ylabel("Kibocsátás (ezer tonna)", fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
# 3. Pontdiagram + Lineáris Regresszió
plt.figure(figsize=(10, 5))
plt.scatter(x, y, color='red', label='Éves kibocsátási adatok (Pontdiagram)', alpha=0.7)
plt.plot(x, y_pred, color='navy', label='Lineáris Trendvonal (Regresszió)', linewidth=2)
# Regressziós egyenlet és R^2 kiírása a diagramra
egyenlet = f"y = {meredekseg:.2f}x + {metszet:.0f}"
r2_kiiras = f"R² = {r_sq:.3f}"
plt.annotate(egyenlet, xy=(0.05, 0.9), xycoords='axes fraction', fontsize=10, color='navy')
plt.annotate(r2_kiiras, xy=(0.05, 0.82), xycoords='axes fraction', fontsize=10, color='navy')
plt.title("Pontdiagram és Lineáris Regresszió (CO₂ Kibocsátás)", fontsize=14)
plt.xlabel("Év", fontsize=12)
plt.ylabel("Kibocsátás (ezer tonna)", fontsize=12)
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()
Vonaldiagram, Pontdiagram és Lináris Regresszió eredmények: